お金ってなあに? ~価値を計測する~
お金についての勉強会の4回目は「価値の計測」について考えていきましょう。

客観的な価値
世の中には様々な商品が溢れています。
食料品や衣料品、不動産や金融商品など、ジャンルも価値も様々で、安い物から高い物まで色々な商品が売られています。
商品が異なれば価値は異なりますし、似たような商品でも価値は異なります。
例えば、同じサイズのテレビがあって、A社のテレビとB社のテレビはどちらが高いの?
と聞かれた時、最初に考えるのは値段を比べる事だと思います。
当然値段が高い方が高いテレビと言う判断になりますし、店によって値段が異なるのなら、A社とB社の一番安い店の値段を比較したり、平均金額を比較したりすると思います。
単純に比較できるのは、「円」と言う計測する単位があるから出来ると言う事ですね。
もし、お金がなかったらこんな比べ方になると思います。
・A社のテレビは、一番安いのは山田電機で牛肉10㎏と交換してくれる
・B社のテレビは、一番安いのは鈴木電機で豚肉15㎏と交換してくれる
となります。
どちらが安いと思いますか?
どちらが安いか調べるには、牛肉と豚肉の価値を調べる必要があります。
・牛肉1㎏は、渡辺商店で缶コーヒー10本と交換してくれる
・豚肉1㎏は、山本商店で缶ジュース10本と交換してくれる
それじゃあ、缶コーヒーと缶ジュースはどちらが安いの?
と永遠に続いていきます。
何かを比較しようとすると、共通する基準がなければ正しく比較が出来ないと言うことですね。
似たような話しは他にもあります。
世界中の人の足の大きさを比較するとき
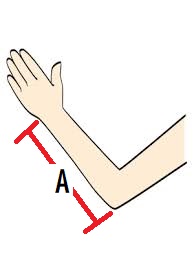
上の図のような腕の「A」の長さは、

足の大きさ「B」の何個分かを調べると
ほとんどの人が、「足の大きさは肘から手首までの長さと同じ」と言う事になります。
この答えだけを見ると、足の大きさは人類共通と言う間違った答えになる可能性があります。
(もちろん腕の長さは人によって異なるので、足の大きさも人によって異なります)
なぜ足の大きさが人類共通と言う答えになってしまったかと言うと、測る基準となるもの(今回の場合は腕の長さ)が人によって異なるからですね。
変わらない基準が必要
長さ、重さ、価値などを測る時、共通する単位が必要になります。
・長さ:メートル(m)
・重さ:グラム(g)
・価値:円(¥)
と言ったように、何を測る場合でも共通する単位が定められているおかげで、共通した会話が出来ます。
長さを測る時は、定規や巻尺を使うと思いますし、重さを量る時は時は重量計を使うと思います。
価値を測る時も、定規や重量計の代わりにお金を使うのです。
お金を使えば、物の価値だけでなく労働や知識と言う形にならない物も測ることができます。
例えば、1時間の労働でも、誰でもできる事と限られた人しか出来ない事で価値の違いを表現できます。
コンビニのバイトは1000円の報酬ですが、英会話スクールの教師は3000円の報酬と言ったように、
「コンビニの店員が出来る人 > 英語の教えると言う事が出来る人」
と言う希少性の違いで報酬が異なる事を、お金と言う物差しでも表現する事ができます。
複数の物をまとめて計測する
お金にまつわる比較で、長者番付と言うのが発表されています。
長者番付のトップの人は数兆円と言う資産を保有していますが、これもお金と言う物差しがあるおかげで比較できます。
資産かと言われる人は、不動産や金融資産や預金、会社などの様々な資産を保有しています。
単純に資産の保有量を公表してもどれくらいの価値があるのかがわかりません。
・山の土地を100㎢、商店街に1000㎡
・IT企業を2つ経営
・電力会社の株を100万株
と言われても、どれくらいの資産なのかがピンとこないですよね。
・金融資産や不動産を合わせて50億円の資産を保有
ならわかりやすいと思います。
このように、色々な資産の評価をお金に換算して、全て足せば簡単に比較ができるようになります。
これが、「価値を計測する」と言う機能です。
まとめ
ここまで説明してきたように、
・お金持ち
・高級車
・高級住宅街
と言うような価値の比較は、お金と言う物差しがあるから簡単に比較ができるという事です。
言い換えてみれば、お金自体に価値があると言うより、色々な価値をお金と言う単位で表現しているという事です。
例えば、「新幹線は時速300km以上で走行する」と言うのは、300kmと言う数字がすごいのではなく、300kmで走行できる新幹線がすごいですよね。
お金も同様で、1億円の資産家と言うのは1億円と言う数字ではなく、1億円と言う資産を持っている事に価値があります。
この表現が伝わりにくいかも知れないので、これからもお金の学校で表現を変えながら説明していこうと思います。
コメントを残す